Η σχέση μεταξύ των αριθμών και της χωρικής αντίληψης

Πριν από περίπου 150 χρόνια ο πρωτοπόρος πολυπράγμων επιστήμονας Φράνσις Γκαλτόν (Sir Francis Galton) έκανε μια πολύ ενδιαφέρουσα παρατήρηση. Στο άρθρο του στο περιοδικό Nature υπό τον τίτλο «Οπτικοποιημένοι Αριθμοί» περιγράφει την ιδιαίτερη ικανότητα που έχουν αρκετά άτομα να οπτικοποιούν μια σειρά αριθμών, τοποθετώντας τους σε μια σειρά στο οπτικό τους πεδίο [1]Galton, F. (1880). Visualised Numerals. Nature, 21(543), 494-495. doi:10.1038/021494e0 . Σύμφωνα με τον Γκαλτόν, εάν κληθούμε να φανταστούμε μια ομάδα αριθμών (π.χ. από το 1 έως το 100), τότε αυτόματα θα φανταστούμε τους αριθμούς σε μία πολύ συγκεκριμένη διάταξη. Κάποιοι θα φαντάζονται τους αριθμούς σε μια γραμμή, με τους μικρούς στο ένα άκρο και τους μεγάλους στο άλλο, άλλοι θα τους φαντάζονται σαν τον κύκλο ενός ρολογιού, άλλοι ως καμπύλες στο χώρο, κτλ.
Μάλιστα, ο Γκαλτόν υπολόγισε πως 1 στους 30 άνδρες και 1 στις 15 γυναίκες –αυτοί με την πιο ισχυρή «φαντασία»- όχι μόνο οπτικοποιούν τους αριθμούς με μια συγκεκριμένη σειρά αλλά και με ίσες αποστάσεις μεταξύ τους. Αυτές τις διαφορετικές νοητικές αναπαραστάσεις αριθμών τις ονόμασε «μορφές». Η συγκεριμένη μελέτη του Γκαλτόν ξεχάστηκε ανάμεσα στις άπειρες δημοσιεύσεις και τα επιστημονικά συγγράμματα τα οποία επιμελήθηκε κατά τη διάρκεια της πολυετούς καριέρας του, και ο ίδιος –δυστυχώς- έμεινε γνωστός κυρίως ως ο εμπνευστής της ιδέας της ευγονικής θεωρίας.
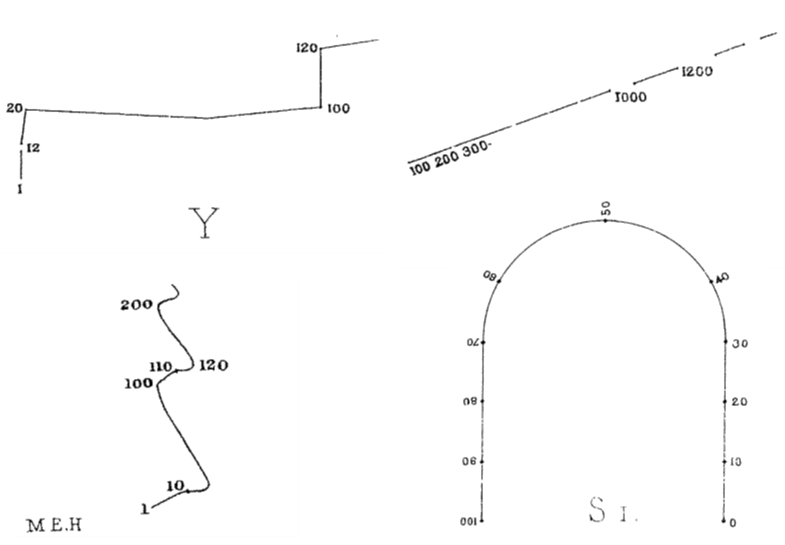
Σχετικά πρόσφατα η επιστημονική κοινότητα άρχισε να δείχνει πολύ έντονο ενδιαφέρον για την νοητική αναπαράσταση των αριθμών στο χώρο, με αποτέλεσμα η έρευνα του Γκαλτόν να ξαναέρθει στην επικαιρότητα. Ένα θεωρητικό πλαίσιο που ενώνει αποτελεσματικά την αντίληψη του χώρου με την αντίληψη των αριθμών θα είχε μεγάλο αντίκτυπο σε αρκετούς τομείς της σύγχρονης ψυχολογίας και των νευροεπιστημών. Η κατανόηση των μηχανισμών της ανθρώπινης αντίληψης και σκέψης, η λειτουργία του ανθρώπινου εγκεφάλου αλλά και η έγκαιρη πρόγνωση ανάπτυξης μαθησιακών δυσκολιών είναι μόνο τρία βασικά παραδείγματα.
Νοητική Αριθμητική Γραμμή
Τις τελευταίες δύο δεκαετίες οι επιστήμονες εξετάζουν με ιδιαίτερο ενδιαφέρον την θεωρία της Νοητικής Αριθμητικής Γραμμής (Mental Number Line). Σύμφωνα με αυτή τη θεωρία, οι άνθρωποι (τουλάχιστον στις δυτικές κουλτούρες) έχουν την τάση να αναπαριστούν νοητικά τους αριθμούς σε αύξουσα σειρά, συνήθως από αριστερά προς τα δεξιά. Υπάρχουν βεβαίως και άτομα που έχουν μια ακριβώς αντίθετη Νοητική Αριθμητική Γραμμή, από δεξιά προς τα αριστερά ή από πάνω προς τα κάτω. Οι λόγοι που υπάρχουν τόσες πολλές νοητικές γραμμές είναι κυρίως κοινωνικοί. Στις χώρες τις Δύσης γράφουμε και διαβάζουμε από αριστερά προς τα δεξιά, ενώ ακόμη και τα όργανα μέτρησης που χρησιμοποιούμε έχουν αυτή τη φορά καταγραφής των αριθμών (π.χ. χάρακας). Αντίθετα, έχει παρατηρηθεί πως σε χώρες της Ανατολής όπου το σύστημα γραφής και ανάγνωσης είναι από τα δεξιά προς τα αριστερά, η Νοητική Αριθμητική Γραμμή ακολουθεί επίσης αυτή τη φορά. Το ίδιο ισχύει και για τους λαούς που γράφουν από πάνω προς τα κάτω (π.χ. Ιαπωνία).
Σε ένα από τα πιο γνωστά πειράματα σε αυτόν τον χώρο είναι η έρευνα των Fisher και των συνεργατών του [2]Fischer, M. H., Castel, A. D., Dodd, M. D., & Pratt, J. (2003). Perceiving numbers causes spatial shifts of attention. Nature Neuroscience, 6(6), 555–556. doi:10.1038/nn1066 . Οι συμμετέχοντες ενός πειράματός τους κλήθηκαν να βλέπουν κάποιους μονοψήφιους αριθμούς και να ενοπίσουν έναν αστερίσκο ο οποίος εμφανιζόταν αμέσως μετά στα δεξιά ή στα αριστερά του οπτικού τους πεδίου, ήταν πιο γρήγοροι στον εντοπισμό των αριστερών στόχων όταν έβλεπαν έναν μικρό αριθμό (π.χ. 1, 2) και των δεξιών στόχων όταν έβλεπαν έναν μεγάλο αριθμό (π.χ. 8,9). Αυτό το εύρημα παρουσιάζει ενδιαφέρον καθώς είναι μια πολύ καλή επίδειξη του πως οι μικροί αριθμοί στρέφουν την προσοχή μας στο αριστερό οπτικό πεδίο και οι μεγάλοι στο δεξί, κάτι το οποίο αποτελεί έμεση επιβεβαίωση της θεωρίας της Νοητικής Αριθμητικής Γραμμής.
Η Νοητική Αριθμητική Γραμμή όμως δεν περιορίζεται στην απλή οπτική αναπαράσταση των αριθμών. Μέσα από σειρά πειραμάτων έχει βρεθεί πως οι αριθμοί τείνουν να σχετίζονται με έναν πιο γενικό τρόπο με τις έννοιες «αριστερά» και «δεξιά». Δεν φανταζόμαστε απλά έναν άξονα όπου οι αριθμοί αναπαρίστανται γραμμικά. Φαίνεται πως γενικότερα υπάρχει μια πιο ισχυρή συσχέτιση των εννοιών του χώρου και των αριθμών. Για παράδειγμα, σειρά πειραμάτων έχει δείξει πως αν κάνουμε μια πιο λεπτομερή ανάλυση πειραμάτων σαν του Fischer, θα δούμε πως τείνουμε να είμαστε γρηγορότεροι όταν απαντάμε με το αριστερό χέρι σε στόχους των οποίων έχει προηγηθεί η εμφάνιση μικρών αριθμών και το αντίστροφο. Με απλά λόγια, απλά και μόνο η θέα ενός μικρού αριθμού αυτόματα στρέφει την προσοχή όχι απλά στο αριστερό μας οπτικό πεδίο, αλλά γενικότερα στον αριστερό μας χώρο.
Αυτό που έχει ιδιαίτερο ενδιαφέρον όμως είναι η διαπίστωση πως η Νοητική Αριθμητική Γραμμή δεν είναι απολύτως σταθερή. Ανάλογα με το περιβάλλον μπορεί να αλλάξει. Όταν επαναλήφθηκε το παραπάνω πείραμα, αλλά ζητήθηκε από συμμετέχοντες να φανταστούν ένα ρολόι και να απαντάνε εάν ο εμφανιζόμενος αριθμός είναι “πριν ή μετά την ώρα 6”, βρήκαν πως η επίδραση των αριθμών αντιστρεφόταν. Οι μεγάλοι αριθμοί έστρεφαν την προσοχή στο αριστερό οπτικό πεδίο (όπου βρίσκονται οι αριθμοί 7-11 στο αναλογικό ρολόι) και οι μικροί στο δεξί (όπου βρίσκονται οι αριθμοί 2-5).
Παρόμοιες αλλαγές της Νοητικής Αριθμητικής Γραμμής παρατηρήθηκαν και όταν πριν από μια επανάληψη του πειράματος του Fischer ζητήθηκε από δίγλωσσους συμμετέχοντες (Ρώσικα – Εβραϊκά) να διαβάσουν ένα κείμενο σε μία από τις δύο γλώσσες. Αυτοί που διάβασαν κείμενο στα Ρώσικα (τα οποία διαβάζονται από αριστερά προς τα δεξιά) τότε παρατηρήθηκε η κλασική σύνδεση μικρών αριθμών με το αριστερό πεδίο και των μεγάλων με το δεξί. Αυτοί που διάβασαν κείμενο στα Εβραϊκά (τα οποία διαβάζονται από δεξιά προς τα αριστερά) είχαν ακριβώς τα αντίθετα αποτελέσματα. Όλα τα παραπάνω πειράματα δείχνουν την ευαίσθητη φύση της Νοητικής Αριθμητικής Γραμμής και πόσο εύπλαστη μπορεί να είναι.
Ταυτόχρονα, παρουσιάζει ενδιαφέρον και ο ρόλος της βραχύχρονης μνήμης στην δημιουργία αυτής της νοητικής αριθμητικής γραμμής. Όταν η βραχύχρονη μνήμη είναι γεμάτη και οι αριθμοί βρίσκονται αναγκαστικά σε μια συγκεκριμένη διάταξη (όπως π.χ. στο πείραμα με το ρολόι) τότε νοητικά ακολουθούμε τους κανόνες και τη φορά διάταξης που ορίζει το απομνημονευμένο μοντέλο. Αντίθετα, όταν η βραχύχρονη μνήμη είναι άδεια, τότε ο εγκέφαλός μας ανασύρει κάποιο μοντέλο οπτικοποίησης των αριθμών από την μακρόχρονη μνήμη, το οποίο συνήθως σχετίζεται με το κοινωνικό και γλωσσικό μας περιβάλλον. Ελλείψει δηλαδή κάποιου μοντέλου που να μας υποδεικνύεται από αυτό που κάνουμε εκείνη τη στιγμή (π.χ. συγκρίνουμε ώρες), ο εγκέφαλός μας αυτόματα χρησιμοποιεί μοντέλα που αξιοποιούμε πιο συχνά στην καθημερινότητά μας.
Χρησιμότητα της θεωρίας της Νοητικής Αριθμητικής Γραμμής
Όπως αναφέρθηκε ήδη, η σχέση μεταξύ αριθμών, οπτικής αντίληψης και προσοχής έχει ιδιαίτερο επιστημονικό ενδιαφέρον γιατί εμπλουτίζει τις γνώσεις μας για τον τρόπο λειτουργίας του ανθρώπινου εγκεφάλου. Αλλά πέρα από την ακαδημαϊκή τους ή τη φιλοσοφική τους αξία, ποια μπορεί να είναι η πρακτική χρησιμότητα των δεδομένων που συλλέγουμε γύρω από αυτό το φαινόμενο; Όταν αποδειχθεί και εδραιωθεί μια συγκεκριμένη και λεπτομερής θεωρία για τη σχέση της αριθμητικής και της οπτικής αντίληψης, αλλά και για το πως αυτή εξελίσσεται στο χρόνο, τότε οι γνώσεις μας θα μπορούσαν να οδηγήσουν στην δημιουργία διαφόρων διαγνωστικών τεστ μαθησιακών δυσκολιών που σχετίζονται με τους αριθμούς, όπως για παράδειγμα η δυσαριθμησία. Εάν μπορούσαμε να τρέχουμε ένα γρήγορο τεστ οπτικής αντίληψης σε παιδιά σχολικής ηλικίας και βάσει αυτού υπολογίζαμε με κάποιο σημαντικό βαθμό αξιοπιστίας την πιθανότητα το παιδί να αναπτύξει μαθησιακές διαταραχές τότε θα μπορούσαμε να επέμβουμε πιο γρήγορα και άμεσα ώστε να αντιμετωπίσουμε το όποιο πρόβλημα πριν αυτό γιγαντωθεί και δημιουργήσει περισσότερα εμπόδια στην γνωστική ανάπτυξη του παιδιού.
Επιπλέον, η σύνδεση αριθμητικής αντίληψης και αντίληψης χώρου δεν αποκλείεται να οδηγήσει σε νέες μεθόδους αντιμετώπισης των περιπτώσεων εγκεφαλικών βλαβών και αφασιών που επηρεάζουν τις χωρικοοπτικές ικανότητες των ασθενών. Για παράδειγμα, δεν αποκλείεται η συνεχής ενδυνάμωση ή και η εκμάθηση μαθηματικών ικανοτήτων να βοηθάει στην ταυτόχρονη ενδυνάμωση της οπτικής αντίληψης. Τέτοιου είδους γνώσεις είναι σημαντικές στους επαγγελματίες που ασχολούνται με την θεραπεία ατόμων που έχουν υποστεί εγκεφαλικές βλάβες που επηρεάζουν τις γνωστικές τους ικανότητες. Φυσικά, προς το παρόν όλες οι πιθανές πρακτικές εφαρμογές αυτών των ερευνών παραμένουν μια απλή υπόθεση, Πρώτα θα πρέπει να μελετηθούν όλες οι λεπτομέρειες γύρω από τις σχέσεις αυτών των δύο γνωστικών ικανοτήτων.
Τέλος, οι γνώσεις που αποκτούμε από αυτόν τον τομέα έρευνας μπορούν (και πρέπει) να χρησιμοποιηθούν από τους διδάσκοντες τόσο σε παιδιά με ειδικές μαθησιακές διαταραχές, όσο και σε παιδιά ενός μέσου σχολείου. Εάν πράγματι υπάρχει αυτή η σύνδεση αντίληψης χώρου και αριθμών, μια πολύ καλή ιδέα θα ήταν ο εμπλουτισμός της εκμάθησης μαθηματικών με ασκήσεις που ενεργοποιούν τις χωρικο-οπτικές ικανότητες των παιδιών.
Ίσως εν τέλει να είναι πολύ πιο αποτελεσματικό τα μαθηματικά να διδάσκονται όχι απλά με μεθόδους απομνημόνευσης κανόνων, αλλά με μεθόδους που συνδυάζουν απομνημόνευση, οπτική αντίληψη και γενικά που υποχρεώνουν τον μαθητή να προσπαθήσει να οπτικοποιήσει τις σχέσεις μεταξύ των αριθμών. Εξάλλου, δεν θα πρέπει να ξεχνάμε πως όσοι ασχολούνται με τις θετικές επιστήμες έχουν πολύ συχνά την τάση να οπτικοποιούν και να ομαδοποιούν αριθμούς, μαθηματικές πράξεις και συσχετίσεις μεταξύ συνόλων. Ίσως έχει έρθει η ώρα να αρχίσουμε να εφαρμόζουμε αυτές τις πρακτικές και στον γενικό πληθυσμό με έναν πιο συστηματικό τρόπο.
Εισαγωγική Εικόνα
- Προκατάληψη: προϊόν και κοινωνικής μάθησης - 12 Ιουλίου, 2024
- Μπορεί μια δοκιμασία οπτικής αντίληψης να εντοπίσει τα βρέφη με αυξημένο κίνδυνο ανάπτυξης αυτισμού; - 12 Ιουνίου, 2024
- Έφηβοι που έχουν πέσει θύμα εκφοβισμού έχουν αυξημένες πιθανότητες να εμφανίσουν ψυχωτικά συμπτώματα - 22 Φεβρουαρίου, 2024
Πηγές / Διαβάστε περισσότερα





